
PDF Publication Title:
Text from PDF Page: 102
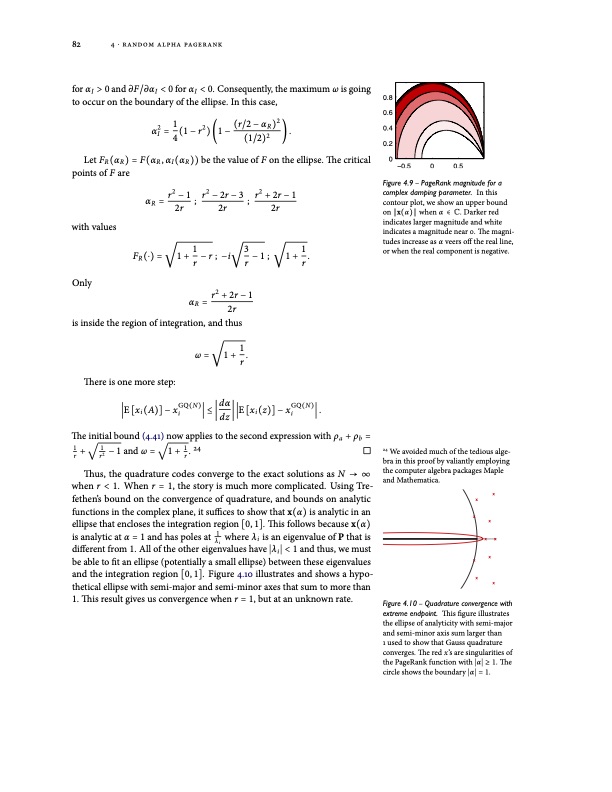
82 4 ⋅ random alpha pagerank for αI > 0 and ∂F/∂αI < 0 for αI < 0. Consequently, the maximum ω is going to occur on the boundary of the ellipse. In this case, 2 1 2 (r/2 − αR)2 αI= (1−r)(1− 2 ). 4 (1/2) LetFR(αR)=F(αR,αI(αR))bethevalueofFontheellipse.Thecritical points of F are with values Only 0.8 0.6 0.4 0.2 0 r2 −1 r2 −2r−3 αR=; ; Figure 4.9 – PageRank magnitude for a complexdampingparameter. Inthis contour plot, we show an upper bound on ∥x(α)∥ when α ∈ C. Darker red indicates larger magnitude and white indicates a magnitude near 0. The magni- tudes increase as α veers off the real line, or when the real component is negative. FR(⋅)= 1+ 131 −r; −i −1; 1+ . rrr r2 + 2r − 1 is inside the region of integration, and thus √ 1 ω=1+. r r2 +2r−1 2r 2r 2r √√√ There is one more step: ∣E [xi (A)] − xi ∣ ≤ ∣ ∣ ∣E [xi (z)] − xi αR = 2r GQ(N) dα GQ(N) dz ∣ . The initial bound (4.41) now applies to the second expression with ρa + ρb = √√ 1+ 1 −1andω= 1+1.24 24 We avoided much of the tedious alge- bra in this proof by valiantly employing the computer algebra packages Maple and Mathematica. X X X X XX X X X X Figure 4.10 – Quadrature convergence with extremeendpoint. Thisfigureillustrates the ellipse of analyticity with semi-major and semi-minor axis sum larger than 1 used to show that Gauss quadrature converges. The red x’s are singularities of the PageRank function with ∣α∣ ≥ 1. The circle shows the boundary ∣α∣ = 1. rr2 r Thus, the quadrature codes converge to the exact solutions as N → ∞ when r < 1. When r = 1, the story is much more complicated. Using Tre- fethen’s bound on the convergence of quadrature, and bounds on analytic functions in the complex plane, it suffices to show that x(α) is analytic in an ellipse that encloses the integration region [0, 1]. This follows because x(α) be able to fit an ellipse (potentially a small ellipse) between these eigenvalues and the integration region [0, 1]. Figure 4.10 illustrates and shows a hypo- thetical ellipse with semi-major and semi-minor axes that sum to more than 1. This result gives us convergence when r = 1, but at an unknown rate. is analytic at α = 1 and has poles at 1 where λ is an eigenvalue of P that is i different from 1. All of the other eigenvalues have ∣λi ∣ < 1 and thus, we must λi −0.5 0 0.5PDF Image | MODELS AND ALGORITHMS FOR PAGERANK SENSITIVITY
PDF Search Title:
MODELS AND ALGORITHMS FOR PAGERANK SENSITIVITYOriginal File Name Searched:
gleich-pagerank-thesis.pdfDIY PDF Search: Google It | Yahoo | Bing
Cruise Ship Reviews | Luxury Resort | Jet | Yacht | and Travel Tech More Info
Cruising Review Topics and Articles More Info
Software based on Filemaker for the travel industry More Info
The Burgenstock Resort: Reviews on CruisingReview website... More Info
Resort Reviews: World Class resorts... More Info
The Riffelalp Resort: Reviews on CruisingReview website... More Info
| CONTACT TEL: 608-238-6001 Email: greg@cruisingreview.com | RSS | AMP |