
PDF Publication Title:
Text from PDF Page: 110
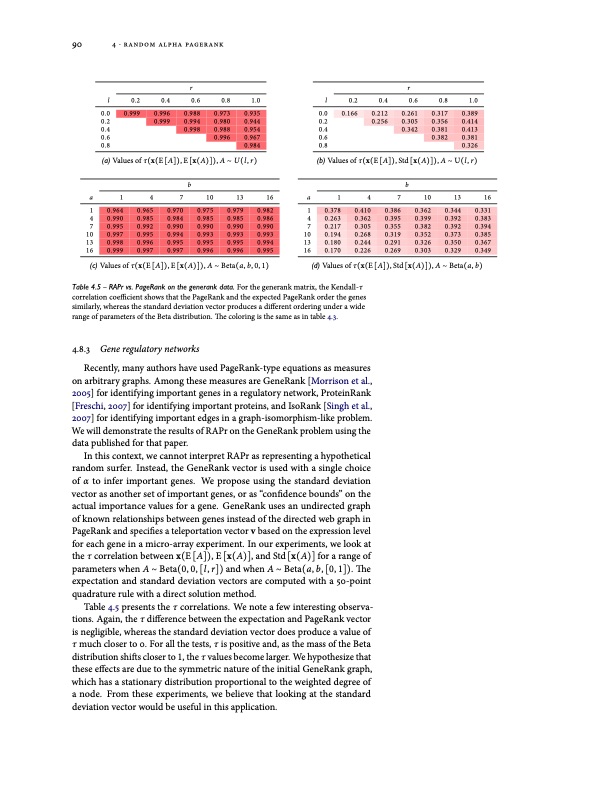
90 4 ⋅ random alpha pagerank rr l 0.0 0.2 0.4 0.6 0.8 0.2 0.4 0.6 0.999 0.996 0.988 0.999 0.994 0.998 0.8 0.973 0.980 0.988 0.996 1.0 0.935 0.944 0.954 0.967 0.984 l 0.2 0.4 0.6 0.8 0.0 0.166 0.212 0.261 0.317 0.2 0.256 0.305 0.356 0.4 0.342 0.381 0.6 0.382 0.8 1.0 0.389 0.414 0.413 0.381 0.326 (a) Values of τ(x(E [A]), E [x(A)]), A ∼ U (l , r) bb 1 4 7 10 13 16 0.964 0.965 0.970 0.975 0.979 0.982 0.990 0.985 0.984 0.985 0.985 0.986 0.995 0.992 0.990 0.990 0.990 0.990 0.997 0.995 0.994 0.993 0.993 0.993 10 0.194 0.268 0.319 0.352 0.373 0.385 0.998 0.996 0.995 0.995 0.995 0.994 13 0.180 0.244 0.291 0.326 0.350 0.367 0.999 0.997 0.997 0.996 0.996 0.995 16 0.170 0.226 0.269 0.303 0.329 0.349 a 1 4 7 10 13 16 (b) Values of τ(x(E [A]), Std [x(A)]), A ∼ U(l , r) a 1 4 7 10 13 16 1 0.378 0.410 0.386 0.362 0.344 0.331 4 0.263 0.362 0.395 0.399 0.392 0.383 7 0.217 0.305 0.355 0.382 0.392 0.394 (c) Values of τ(x(E [A]), E [x(A)]), A ∼ Beta(a, b, 0, 1) (d) Values of τ(x(E [A]), Std [x(A)]), A ∼ Beta(a, b) Table 4.5 – RAPr vs. PageRank on the generank data. For the generank matrix, the Kendall-τ correlation coefficient shows that the PageRank and the expected PageRank order the genes similarly, whereas the standard deviation vector produces a different ordering under a wide range of parameters of the Beta distribution. The coloring is the same as in table 4.3. 4.8.3 Gene regulatory networks Recently, many authors have used PageRank-type equations as measures on arbitrary graphs. Among these measures are GeneRank [Morrison et al., 2005] for identifying important genes in a regulatory network, ProteinRank [Freschi, 2007] for identifying important proteins, and IsoRank [Singh et al., 2007] for identifying important edges in a graph-isomorphism-like problem. We will demonstrate the results of RAPr on the GeneRank problem using the data published for that paper. In this context, we cannot interpret RAPr as representing a hypothetical random surfer. Instead, the GeneRank vector is used with a single choice of α to infer important genes. We propose using the standard deviation vector as another set of important genes, or as “confidence bounds” on the actual importance values for a gene. GeneRank uses an undirected graph of known relationships between genes instead of the directed web graph in PageRank and specifies a teleportation vector v based on the expression level for each gene in a micro-array experiment. In our experiments, we look at the τ correlation between x(E [A]), E [x(A)], and Std [x(A)] for a range of parameters when A ∼ Beta(0, 0, [l , r]) and when A ∼ Beta(a, b, [0, 1]). The expectation and standard deviation vectors are computed with a 50-point quadrature rule with a direct solution method. Table 4.5 presents the τ correlations. We note a few interesting observa- tions. Again, the τ difference between the expectation and PageRank vector is negligible, whereas the standard deviation vector does produce a value of τ much closer to 0. For all the tests, τ is positive and, as the mass of the Beta distribution shifts closer to 1, the τ values become larger. We hypothesize that these effects are due to the symmetric nature of the initial GeneRank graph, which has a stationary distribution proportional to the weighted degree of a node. From these experiments, we believe that looking at the standard deviation vector would be useful in this application.PDF Image | MODELS AND ALGORITHMS FOR PAGERANK SENSITIVITY
PDF Search Title:
MODELS AND ALGORITHMS FOR PAGERANK SENSITIVITYOriginal File Name Searched:
gleich-pagerank-thesis.pdfDIY PDF Search: Google It | Yahoo | Bing
Cruise Ship Reviews | Luxury Resort | Jet | Yacht | and Travel Tech More Info
Cruising Review Topics and Articles More Info
Software based on Filemaker for the travel industry More Info
The Burgenstock Resort: Reviews on CruisingReview website... More Info
Resort Reviews: World Class resorts... More Info
The Riffelalp Resort: Reviews on CruisingReview website... More Info
| CONTACT TEL: 608-238-6001 Email: greg@cruisingreview.com | RSS | AMP |