
PDF Publication Title:
Text from PDF Page: 128
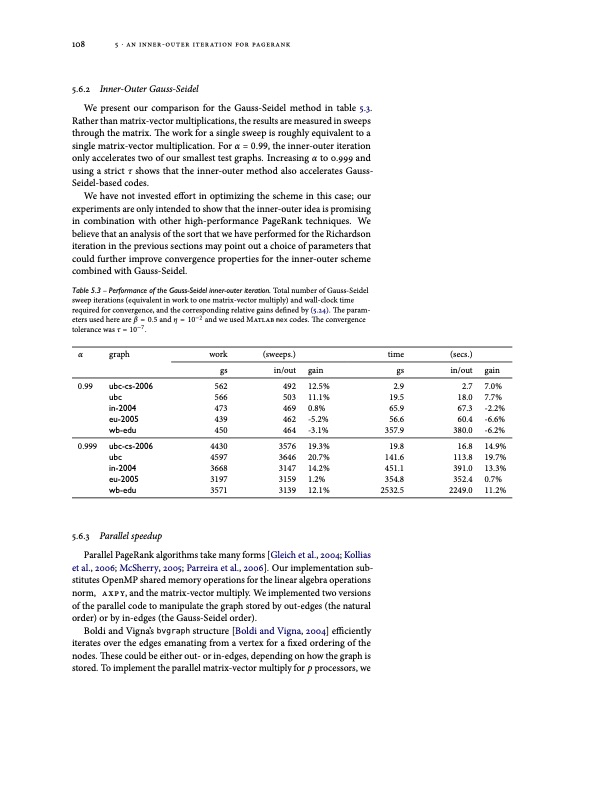
108 5 ⋅ an inner-outer iteration for pagerank 5.6.2 Inner-Outer Gauss-Seidel We present our comparison for the Gauss-Seidel method in table 5.3. Rather than matrix-vector multiplications, the results are measured in sweeps through the matrix. The work for a single sweep is roughly equivalent to a single matrix-vector multiplication. For α = 0.99, the inner-outer iteration only accelerates two of our smallest test graphs. Increasing α to 0.999 and using a strict τ shows that the inner-outer method also accelerates Gauss- Seidel-based codes. We have not invested effort in optimizing the scheme in this case; our experiments are only intended to show that the inner-outer idea is promising in combination with other high-performance PageRank techniques. We believe that an analysis of the sort that we have performed for the Richardson iteration in the previous sections may point out a choice of parameters that could further improve convergence properties for the inner-outer scheme combined with Gauss-Seidel. Table 5.3 – Performance of the Gauss-Seidel inner-outer iteration. Total number of Gauss-Seidel sweep iterations (equivalent in work to one matrix-vector multiply) and wall-clock time required for convergence, and the corresponding relative gains defined by (5.24). The param- eters used here are β = 0.5 and η = 10−2 and we used Matlab mex codes. The convergence tolerance was τ = 10−7 . α graph work (sweeps.) gs in/out gain 12.5% 11.1% 0.8% -5.2% -3.1% 19.3% 20.7% 14.2% 1.2% 12.1% time (secs.) gs in/out 2.9 2.7 19.5 18.0 65.9 67.3 56.6 60.4 357.9 380.0 19.8 16.8 141.6 113.8 451.1 391.0 354.8 352.4 2532.5 2249.0 gain 7.0% 7.7% -2.2% -6.6% -6.2% 14.9% 19.7% 13.3% 0.7% 11.2% 0.99 ubc-cs-2006 ubc 566 503 in-2004 473 469 eu-2005 439 462 wb-edu 450 464 0.999 ubc-cs-2006 ubc 4597 3646 in-2004 3668 3147 eu-2005 3197 3159 wb-edu 3571 3139 5.6.3 Parallel speedup 562 492 4430 3576 Parallel PageRank algorithms take many forms [Gleich et al., 2004; Kollias et al., 2006; McSherry, 2005; Parreira et al., 2006]. Our implementation sub- stitutes OpenMP shared memory operations for the linear algebra operations norm, axpy, and the matrix-vector multiply. We implemented two versions of the parallel code to manipulate the graph stored by out-edges (the natural order) or by in-edges (the Gauss-Seidel order). Boldi and Vigna’s bvgraph structure [Boldi and Vigna, 2004] efficiently iterates over the edges emanating from a vertex for a fixed ordering of the nodes. These could be either out- or in-edges, depending on how the graph is stored. To implement the parallel matrix-vector multiply for p processors, wePDF Image | MODELS AND ALGORITHMS FOR PAGERANK SENSITIVITY
PDF Search Title:
MODELS AND ALGORITHMS FOR PAGERANK SENSITIVITYOriginal File Name Searched:
gleich-pagerank-thesis.pdfDIY PDF Search: Google It | Yahoo | Bing
Cruise Ship Reviews | Luxury Resort | Jet | Yacht | and Travel Tech More Info
Cruising Review Topics and Articles More Info
Software based on Filemaker for the travel industry More Info
The Burgenstock Resort: Reviews on CruisingReview website... More Info
Resort Reviews: World Class resorts... More Info
The Riffelalp Resort: Reviews on CruisingReview website... More Info
| CONTACT TEL: 608-238-6001 Email: greg@cruisingreview.com | RSS | AMP |