
PDF Publication Title:
Text from PDF Page: 129
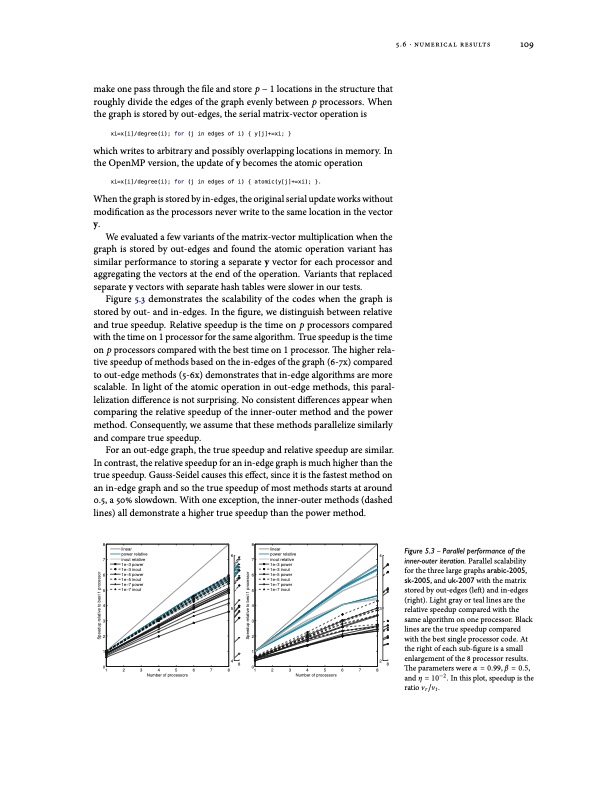
make one pass through the file and store p − 1 locations in the structure that roughly divide the edges of the graph evenly between p processors. When the graph is stored by out-edges, the serial matrix-vector operation is xi=x[i]/degree(i); for (j in edges of i) { y[j]+=xi; } which writes to arbitrary and possibly overlapping locations in memory. In the OpenMP version, the update of y becomes the atomic operation xi=x[i]/degree(i); for (j in edges of i) { atomic(y[j]+=xi); }. When the graph is stored by in-edges, the original serial update works without modification as the processors never write to the same location in the vector y. We evaluated a few variants of the matrix-vector multiplication when the graph is stored by out-edges and found the atomic operation variant has similar performance to storing a separate y vector for each processor and aggregating the vectors at the end of the operation. Variants that replaced separate y vectors with separate hash tables were slower in our tests. Figure 5.3 demonstrates the scalability of the codes when the graph is stored by out- and in-edges. In the figure, we distinguish between relative and true speedup. Relative speedup is the time on p processors compared with the time on 1 processor for the same algorithm. True speedup is the time on p processors compared with the best time on 1 processor. The higher rela- tive speedup of methods based on the in-edges of the graph (6-7x) compared to out-edge methods (5-6x) demonstrates that in-edge algorithms are more scalable. In light of the atomic operation in out-edge methods, this paral- lelization difference is not surprising. No consistent differences appear when comparing the relative speedup of the inner-outer method and the power method. Consequently, we assume that these methods parallelize similarly and compare true speedup. For an out-edge graph, the true speedup and relative speedup are similar. In contrast, the relative speedup for an in-edge graph is much higher than the true speedup. Gauss-Seidel causes this effect, since it is the fastest method on an in-edge graph and so the true speedup of most methods starts at around 0.5, a 50% slowdown. With one exception, the inner-outer methods (dashed lines) all demonstrate a higher true speedup than the power method. 88 64 77 66 55 44 53 33 22 11 42 01 2 3 4 5 6 7 88 01 2 3 4 5 6 7 88 Number of processors Number of processors Figure 5.3 – Parallel performance of the inner-outer iteration. Parallel scalability for the three large graphs arabic-2005, sk-2005, and uk-2007 with the matrix stored by out-edges (left) and in-edges (right). Light gray or teal lines are the relative speedup compared with the same algorithm on one processor. Black lines are the true speedup compared with the best single processor code. At the right of each sub-figure is a small enlargement of the 8 processor results. Theparameterswereα=0.99,β=0.5, and η = 10−2. In this plot, speedup is the ratio vr/vt. 5.6 ⋅ numerical results 109 linear power relative inout relative 1e−3 power 1e−3 inout 1e−5 power 1e−5 inout 1e−7 power 1e−7 inout linear power relative inout relative 1e−3 power 1e−3 inout 1e−5 power 1e−5 inout 1e−7 power 1e−7 inout Speedup relative to best 1 processor Speedup relative to best 1 processorPDF Image | MODELS AND ALGORITHMS FOR PAGERANK SENSITIVITY
PDF Search Title:
MODELS AND ALGORITHMS FOR PAGERANK SENSITIVITYOriginal File Name Searched:
gleich-pagerank-thesis.pdfDIY PDF Search: Google It | Yahoo | Bing
Cruise Ship Reviews | Luxury Resort | Jet | Yacht | and Travel Tech More Info
Cruising Review Topics and Articles More Info
Software based on Filemaker for the travel industry More Info
The Burgenstock Resort: Reviews on CruisingReview website... More Info
Resort Reviews: World Class resorts... More Info
The Riffelalp Resort: Reviews on CruisingReview website... More Info
| CONTACT TEL: 608-238-6001 Email: greg@cruisingreview.com | RSS | AMP |